Методика изучения нумерации чисел от 1 до 10

Выделение темы “Десяток” в особый концентр объясняется рядом причин:

• I. Десять – основание десятичной системы счисления, поэтому числа от 1 до 10 образуются в результате счета простых единиц (без использования других разрядных единиц).
• II. Для обозначения каждого из чисел первого десятка применяется в устной речи особое слово, а на письме – особый знак.
• III. Случаи сложения и вычитания в пределах 10 являются табличными, они заучиваются наизусть.

Задачи изучения нумерации:

1. Продолжить работу, начатую в подготовительный период.
2. Ввести числа.
3. Познакомить учащихся с математической символикой, знаками “.
   > “,”< “,” + “,”=”,”-“, показать возможность их использования.
4. азъяснить принцип образования натурального ряда чисел.
5. Познакомить учащихся с числом и цифрой 0.
6. ести целенаправленную работу по усвоению состава чисел.

В результате изучения темы в сознании детей должны отложиться не отдельные факты, характеризующие каждое число в отдельности , а как может быть обобщения , т.е. например , дети должны усвоить не то получено данное число , но и вообще как может быть получено любое число последующее за данным и т.д. , с этой целью в учебнике числа рассматриваются не изолированно , а отрезками натурального ряда:

1,2; 1,2,3; 1,2,3,4;…

Уроки, посвященные знакомству с числами:

• полезно начинать с повторения как получали ранее рассматриваемые числа (3=2+1=4-1);
• прибавлением единицы получить рассматриваемое число (использовать наглядность, наборный материал, пересчитывание);
• показ цифры и нахождение ее учащимися в классе;
• запись 2+1=3 с использованием карточек с печатными цифрами и знаками;
• сравнение на наглядном материале 4>3; 3< 4 ; 4=4;
• запись письменная.

Образование чисел раскрывается с помощью таких упражнений:

1. Присчитывание (к двум палочкам присоединяют одну и выясняют, сколько стало всего и т.д.).
2. Отсчитывание (от 4 палочек отодвигают одну и выясняют, сколько осталось).
3. Черчение и измерение отрезков, длина которых выражается целым числом сантиметров (начертить отрезок длиной 4 см увеличить его на 1 см ниже начертить отрезок на 1 см короче, выясняют какой длины получился отрезок).

Знание состава числа чисел первого десятка лежит в основе сложения и вычитания. Схема изучения состава числа следующая: берутся два любых множества предметов или их моделей эти предметы по одному перекладываются из одного множества в другое.

В учебниках много упражнений на состав числа:

• составление и решение примеров задач по картинкам.

? ????
????

• упражнения в составлении примеров с заданным ответом (с опорой на рисунок)
• показ состава числа с помощью кассы и разрезных цифр:
• заполнение таблицы состава числа

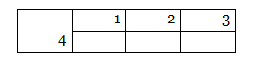
• составление по одному и тому же рисунку двух примеров на сложение и вычитание.

Эти вопросы имеют большое значение при изучении сложения и вычитания в пределах 10 и 100, однако, не следует заставлять детей, чтобы они усвоили на память состав каждого из числе в пределах 10 (6,7,8,9,10). А вот для чисел 1,2,3,4,5 надо выполнить очень много упражнений, чтобы дети твердо усвоили на память состав чисел, обязательно при этом применяя наглядность вначале , а затем и без нее, на память.

Эти знаки можно ввести так: предложить детям нарисовать слева 1 флажок, справа 1 флажок, затем справа нарисовать еще один флажок. Дети скажут, что слева флажков больше чем справа. Далее обозначают число флажков цифрой н устанавливают, что число 1 < 2 и учитель показывает знак “<” говоря , что он обозначает слово “меньше” , дальше появляется запись 1 < 2 , дети учатся читать ее: ” Один меньше, чем два”. Также рассматривается 2 > 1 , 2=2 . Затем учащиеся упражняются в чтении неравенств и равенств по учебнику, сравнивают числа и записывают полученные равенства и неравенства в тетради.

Чтобы учащиеся запомнили написание самих знаков и не путали, “>” или “<” полезно на видном месте в классе вывесить таблицу с образцами. Полезно обратить внимание детей на то, что записи читают слева направо. Полезно, воспользоваться следующим мнемоническим правилом: ” знак < направлен острием к меньшему числу ” ( клювики птенцов).

При изучении первых пяти чисел учащиеся подходят к обобщению: каждое следующее число больше предыдущего на единицу, а каждое предыдущее меньше последующего на 1. Поэтому при срав нении чисел постепенно переходят от сравнения совокупностей к выяснению места сравниваемых чисел в натуральном ряду: 6 больше, чем 5, потому что при счете 6 называют после 5; 5 < 6 , потому , что при счете 5 называют перед числом 6 .

Изучение отрезка натурального ряда сводится к усвоению учащимися той закономерности, которая лежит в основе построения натурального ряда. Для усвоения этой закономерности в методики обучения младших школьников используется различные подходы.

При этом на каждом отрезке натурального ряда выполняются однотипные упражнения. В результате выполнения этих упражнений на каждом отрезке натурального ряда чисел связанных с получением следующего из предыдущего и обратно дети убеждаются в том , что числа упорядочены по величине.

Одновременное введение нового числа и цифры его обозначающей затрудняет осознание различий между числом и цифрой. Запись равенств осуществляется по образцу и никак не соотносит их с понятием арифметических действий сложения и вычитания. Понятия “больше на”, “меньше на” используются только для случая присчитывания и отсчитывания по 1.

Рассмотрим подход Истоминой, при котором дети переходят от счета предметов к записи цифр. Составной частью этого перехода является целенаправленная работа по формированию у детей представлений о количественном и порядковом числе и сознательного усвоения операцией счета.

После того, как они научатся писать все цифры от 1 до 9, им предлагается записать весь отрезок натурального ряда чисел от 1 до 9, Для этой цели детям дается задание: рисуем 9 грибов.

Таким образом, нумеруя грибы, дети получают отрезок натурального ряда (не следует вводить термин – отрезок натурального ряда). Математическую основу действий учащихся при изучен отрезка натурального ряда от 1 до 9 составляет связь чисел с конечными множествами. Для усвоения натурального ряда чисел и принципа его образования они постепенно обращаются к действиям с предметами, рассматривая различные ситуации. Это позволяет детям выполнять присчитывание и отсчитывание по единице.

Для закрепления знаний учащихся числового ряда полезно предложить учащимся следующие задания:

• назовите пропущенные числа: 1,2,3 , — , — , 6 , — ‘ — ‘ — ‘ 10;
• присчитывайте по одному, начиная с 3 ;
  отсчитывайте по одному, начиная с 7;
• назовите числа которые:
• следуют за 5;
• предшествуют 7;
• являются ” соседями ” числа 3;
• стоят между 5 и 7;
• расположите данные числа в порядке счета: 5,7,3,1,2;
• расположите данные числа в порядке, обратном счету: 3,9,7,1,5,6.

В результате учащиеся должны научиться вести счет в прямом и
обратном порядке, сразу без счета указывать число, предшествующее данному и непосредственно следующее за ним.

Один из подходов введения числа 0 связан c установлением соответствия между числовой фигурой и цифрой, обозначающей количество предметов

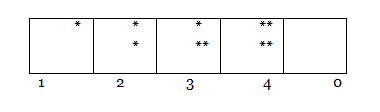
Этим подходом можно пользоваться еще до изучения сложения и вычитания на этапе формирования представлений о количественном числе. Другой методический прием знакомит учащихся с нулем как результатом вычитания. Понятие об этом числе дети получают, выполняя ряд упражнений в отсчитывании предметов по одному до тех пор, пока не останется ни одного.

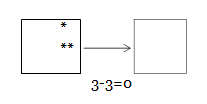
Затем вводится обозначение числа 0 цифрой. Следует иметь ввиду, что при таком введении числа 0 у детей может сложится неправильное представление о числе как результате вычитания. Чтобы этого не случилось необходимо рассмотреть как можно больше различных ситуаций.

Например: что изменилось?

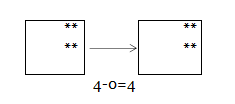
Кроме того, можно познакомить с членом 0 как с компонентом арифметических действий.
Например: что изменилось?

Далее число 0 сравнивается с числом 1, 0 < 1 . На основе таких упражнений устанавливают, что в ряду чисел 0 должен стоять перед числом 1 , т.к. 0 < 1 на 1.

В целях подготовки к изучению сложения и вычитания следует показать, что прибавлять и вычитать можно различные числа, а не только 1, поэтому уже при изучении нумерации рассматривают все случаи сложения и вычитания в пределах 5, а также отдельные случаи в пределах.

10. Результаты действий находят путем соответствующих операций над множествами, что помогает детям понять конкретный смысл этих действий . После того как дети найдут результат сложения, сразу выясняют как, получается этот результат. В результате дети запоминают состав числа.

Состав чисел от 6 до 10 усваивается позже. Основой для изучения операции сложения является практическое действие по объединению двух данных множеств предметов. Пример: учитель предлагает учащимся взять предметные картинки с изображением трех кленовых листьев, затем картинки с дубовыми листьями и спрашивает, сколько листьев они взяли.

При изучении операции вычитания надо начинать с упражнений на выделение некоторой части множества по определенному признаку и по следующему удалению этой части. Например: учащимся предлагается картинка, на которой изображены голуби и воробьи, причем отдельными группами.

Учитель спрашивает, сколько птиц изображено на картинке, сколько среди них голубей. Затем говорит, что голуби улетели, и закрывает соответствующую часть картинки. Учащимся предлагается ответить, сколько птиц осталось.

Наглядные пособия, используемые при изучении чисел первого десятка.

1. предметные пособия:

• предметы окружающей действительности;
• спец, изготовленные предметы для счета (палочки, счеты, ариф . ящик ) ;
• геометрические фигуры;
• трафареты фруктов, овощей;
• детское домино.

2. иллюстративные пособия:

• набор предметных картинок с изображением предметов;
• изображение предметов от 1 до 10;
• картинки с изображением как однородных, так и разнородных предметов, объединенных каким – либо сюжетом;
• таблица “Числовая лесенка” (убывающая или возрастающая);
• набор подвижных цифр и знаков;
• таблица правильного написания цифр;
• монетные кассы;
• серия таблиц по теме “Нумерация чисел первого десятка” Дидактические игры.
• “зрительный диктант” (выкладывание по образцу рисунков из палочек, кружков и т.п.) -рисование орнаментов;
• счет цепочкой (прямой и обратный с любого числа);
• “детское домино”.
• “найди пару”;
• “городские автоматы “(набор нужной суммы с помощью монет различного достоинства).